いろいろ (a+b+c)3 ka formula 163009-(a+b+c)2 ka formula
Using determinants, we can write the result as a × b = a 2 a 3 b 2 b 3 i − a 1 a 3 b 1 b 3 j a 1 a 2 b 1 b 2 k Looking at the formula for the 3 × 3 determinant, we see that the formula for a cross product looks a lot like the formula for the 3 × 3 determinantExample 3 A = {a, b, c, d, e}, B = {x, y, z} and C = {a, e, x} find the value of n(AUBUC) Solution n(AUBUC)=n(A)n(B) n(C)n(AnB)n(BnC)n(CnA)n(AnBnC) n (A) = 5 n (B) = 3 n (C) = 3 A n B = {a, b, c, d, e} n {x, y, z} = { } n (A n B) = 0 B n C = {x, y, z} n {a, e, x} = {x} n (B n C) = 1The Triangle Formula are given below as, Perimeter of a triangle = a b c \Area\;

Ncert Class 9 Maths Lab Manual Verify The Algebraic Identity A B C A B C 2ab 2bc 2ca Cbse Tuts
(a+b+c)2 ka formula
(a+b+c)2 ka formula-A 3 b 3 = (a b) (a 2 b 2 − ab) (a b c) 3 = a 3 b 3 c 3 3(a b)(b c)(c a) a 3 b 3 c 3 − 3abc = (a b c) (a 2 b 2 c 2 − ab − bc − ac)Solving for B means to isolate it to one side of the equation, doesn't matter which side A= ABC/3 Start by subtracting A from both sides



3 Ways To Calculate The Circumference Of A Circle Wikihow
MATHEMATICAL FORMULAE Algebra MATHEMATICAL FORMULAE Algebra 1 (ab)2=a22abb2;a2b2=(ab)2−2ab 2 (a−b)2=a2−2abb;a2b2=(a−b)22ab 3 (abc)2=a2b2c22(abbcca) 4 (ab)3=a3b33ab(ab);a3b3=(ab)−3ab(ab) 5(a b c) 2 = a b (c) 2 = a 2 b 2 (c) 2 2ab 2 (b) (c) 2 (c) (a) = a 2 b 2 c 2 2ab – 2bc 2ca Therefore, (a b c) 2 = a 2 b 2 c 2 2ab – 2bc 2ca (a b c) 2 = a ( b) c 2 = a 2 (b 2) c 2 2 (a) (b) 2 (b) (c) 2 (c) (a) = a 2 b 2 c 2 – 2ab – 2bc 2ca Therefore, (a b c) 2 = a 2 b 2 c 2 – 2ab – 2bc 2ca(a b c)³ = a³ b³ c³ 3 (a b) (b c) (a c) It can be written as (a b c)³ a³ b³ c³ = 3 (a b) (b c) (a c) (1) Consider the LHS of equation (1), (a b c)³ a³ b³ c³ = a³ b³ c³ 3 ab (a b) 3 bc (b c) 3 ac (a c) 6 abc a³ b³ c³
The formula for Solution To find the formula for Multiply twice and simplify the terms Squaring the whole equation, we can see that the value of (abc)^{2} is Taking 2 common in we get Therefore, the formula for is This formula is used to express the algebraic identity if they are 3 terms given according to the operations involvedThe Triangle Formula are given below as, Perimeter of a triangle = a b c \Area\;(a b) 3 = a 3 b 3 3ab(a b) (a – b) 3 = a 3 – 3a 2 b 3ab 2 – b 3 = a 3 – b 3 – 3ab(a – b) a 3 – b 3 = (a – b)(a 2 ab b 2) a 3 b 3 = (a b)(a 2 – ab b 2) (a b) 4 = a 4 4a 3 b 6a 2 b 2 4ab 3 b 4
A 3 b 3 c 3 3abc = (a b c)(a 2 b 2 c 2 ab bc ca) Where a = 2a, b = 3b and c = 5c Now apply values of a, b and c on the LHS of identity ie a 3 b 3 c 3 3abc = (a b c)(a 2 b 2 c 2 ab bc ca) and we get = (2a 3b 5c) { (2a) 2 (3b) 2 (5c) 2 – (2a)(3b) – (3b)(5c) – (5c)(2a) } Expand the exponential forms and we getLooking at the formula for the $3 \times 3$ determinant, we see that the formula for a cross product looks a lot like the formula for the $3 \times 3$ determinant If we allow a matrix to have the vector $\vc{i}$, $\vc{j}$, and $\vc{k}$ as entries (OK, maybe this doesn't make sense, but this is just as a tool to remember the cross product), theOnly the use of the quadratic formula, as well as the basics of completing the square will be discussed here (since the derivation of the formula involves completing the square) Below is the quadratic formula, as well as its derivation Derivation of the Quadratic Formula From this point, it is possible to complete the square using the relationship that x 2 bx c = (x h) 2 k Continuing the derivation using this relationship


New Page 1



Algebra Formula Definition Formulas And Examples
There are mainy two forms to write the formula of a 3 b 3 c 3 First one is a 3 b 3 c 3 = ( a b c) a 2 b 2 c 2 − a b − b c − a c 3 a b c Second one is a 3 b 3 c 3 = ( a b c) 1 2 ( a − b) 2 ( b − c) 2 ( c − a) 2 3 a b c(a b c) 2 = a b (c) 2 = a 2 b 2 (c) 2 2ab 2 (b) (c) 2 (c) (a) = a 2 b 2 c 2 2ab – 2bc 2ca Therefore, (a b c) 2 = a 2 b 2 c 2 2ab – 2bc 2ca (a b c) 2 = a ( b) c 2 = a 2 (b 2) c 2 2 (a) (b) 2 (b) (c) 2 (c) (a) = a 2 b 2 c 2 – 2ab – 2bc 2ca Therefore, (a b c) 2 = a 2 b 2 c 2 – 2ab – 2bc 2ca(abc) 3 a 3 b 3 c 3 We can choose three "a"'s for the cube in one way C(3,3)=1, or we can choose an a from the first factor and one from the second and one from the third, being the only way to make a3 The coefficient of the cubes is therefore 1 (It's the same for a, b and c, of course) 3a 2 b3a 2 c Next, we consider the a 2 terms We can choose two a's from 3 factors in C(3,2) ways=3



If The Roots Of The Equation A B X 2 B C X C A 0 Then Prove That 2a B C Brainly In
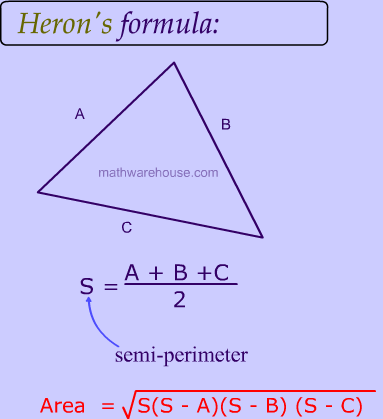


Herons Formula Explained With Pictures Examples And Practice Problems
A= ABC/3 Answer by nerdybill (7384) ( Show Source ) You can put this solution on YOUR website!As stated in the title, I'm supposed to show that (a b c) 3 = a 3 b 3 c 3 (a b c) (a b a c b c)Only the use of the quadratic formula, as well as the basics of completing the square will be discussed here (since the derivation of the formula involves completing the square) Below is the quadratic formula, as well as its derivation Derivation of the Quadratic Formula From this point, it is possible to complete the square using the relationship that x 2 bx c = (x h) 2 k Continuing the derivation using this relationship
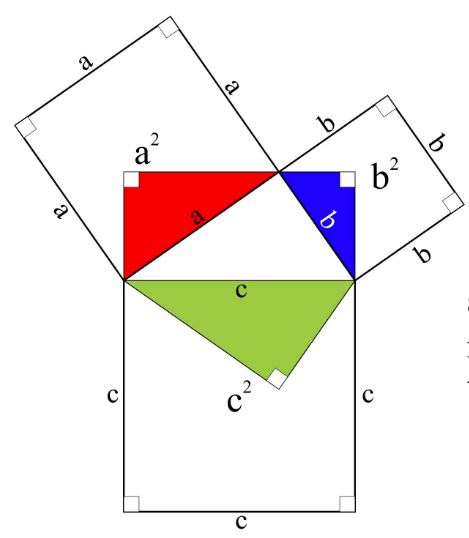


Pythagorean Theorem And Its Many Proofs



Solved Constants Corner Physics 270 Formula Sheet Thermo Chegg Com
Video Lesson Khan Academy Video Quadratic Formula 1;Binomial Theorem (ab)1 = a b ( a b) 1 = a b (ab)2 = a2 2abb2 ( a b) 2 = a 2 2 a b b 2 (ab)3 = a3 3a2b 3ab2 b3 ( a b) 3 = a 3 3 a 2 b 3 a b 2 b 3 (ab)4 = a4 4a3b 6a2b2 4ab3 b4 ( a b) 4 = a 4 4 a 3 b 6 a 2 b 2 4 a b 3 b 4Example 3 A = {a, b, c, d, e}, B = {x, y, z} and C = {a, e, x} find the value of n(AUBUC) Solution n(AUBUC)=n(A)n(B) n(C)n(AnB)n(BnC)n(CnA)n(AnBnC) n (A) = 5 n (B) = 3 n (C) = 3 A n B = {a, b, c, d, e} n {x, y, z} = { } n (A n B) = 0 B n C = {x, y, z} n {a, e, x} = {x} n (B n C) = 1
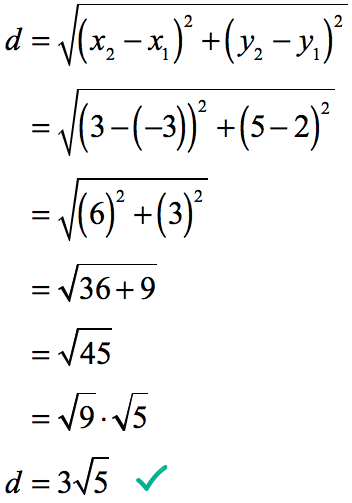


Distance Formula Chilimath


Http Thewe Net Math Gelfand Gelfand3 Pdf
(a b c) 2 = a 2 b 2 c 2 2ab 2bc 2ca (a – b – c) 2 = a 2 b 2 c 2 – 2ab 2bc – 2ca (a b) 3 = a 3 3a 2 b 3ab 2 b 3;Triangle= \frac{1}{2}bh\ Where, b is the base of the triangle h is the height of the triangle If only 2 sides and an internal angle is given then the remaining sides and angles can be calculated using the below formulaSolve an equation of the form a x 2 b x c = 0 by using the quadratic formula x = − b ± √ b 2 − 4 a c 2 a StepByStep Guide Learn all about the quadratic formula with this stepbystep guide Quadratic Formula, The MathPapa Guide;



Mathematics Notes
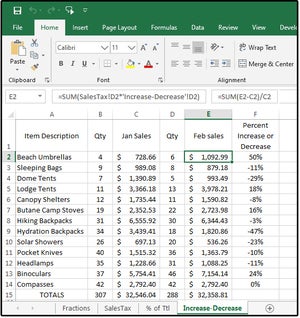


Excel Percentage Formulas Percentage Of Total Percent Increase Or Decrease Sales Tax And More Pcworld
A 3 b 3 c 3 3abc = (a b c)(a 2 b 2 c 2 ab bc ca) Where a = 2a, b = 3b and c = 5c Now apply values of a, b and c on the LHS of identity ie a 3 b 3 c 3 3abc = (a b c)(a 2 b 2 c 2 ab bc ca) and we get = (2a 3b 5c) { (2a) 2 (3b) 2 (5c) 2 – (2a)(3b) – (3b)(5c) – (5c)(2a) } Expand the exponential forms and we get(abc)^3 Formula A Plus B Plus C Whole Square (abc)^3 Proof = a^3 b^3 c^3 6abc 3ab (ab) 3ac (ac) 3bc (bc)Determine the values of a, b, and c for the quadratic equation 4x 2 – 8x = 3 answer choices a = 4, b = 8, c = 3 a = 4, b =8, c =3 a = 4, b = 8, c = 3 a = 4, b = 8, c = 3 s Question 2



Distance Formula Analytic Geometry Video Khan Academy


Boolean Expressions 1 Physical Design Sta Synthesis Dft Automation Flow Dev Verification Services Turnkey Projects
The plural of formula can be either formulas or, under the influence of scientific Latin, formulae In mathematics, a formula generally refers to an identity which equates one mathematical expression to another, with the most important ones being mathematical theorems Syntactically, a formula is an entity which is constructed using the symbols and formation rules of a given logical language For example, determining the volume of a sphere requires a significant amount of integral calculus or itA 3 b 3 c 3 – 3abc = (a b c)(a 2 b 2 c 2 – ab – bc – ca) If a b c = 0, then the above identity reduces to a 3 b 3 c 3 = 3abc Few Other Mathematical FormulaSay, you're typing your letter in C1 and want it to appear in D1 In D1, use the formula =VLOOKUP (C1,AB,2,0) Breaking this down, it means C1 Take the value in C1 AB Look for it in the array composed of columns A trough B 2 Find the match in the 1st column and return the value that's in the 2nd column



Rd Sharma Solutions For Class 8 Chapter 6 Algebraic Expressions And Identities Download Free Pdf



Algebra Formulas A B 3 A B 2 A B C 3 A 3 B 3 Teachoo
Heron's Formula is used to calculate the area of a triangle with the three sides of the triangle You have to first find the semiperimeter of the triangle with three sides and then area can be calculated based on the semiperimeter of the triangle The formula was derived by Hero of Alexendria, a Greek Engineer and Mathematician(abc) 3 a 3 b 3 c 3 We can choose three "a"'s for the cube in one way C(3,3)=1, or we can choose an a from the first factor and one from the second and one from the third, being the only way to make a3 The coefficient of the cubes is therefore 1 (It's the same for a, b and c, of course) 3a 2 b3a 2 c Next, we consider the a 2 terms We can choose two a's from 3 factors in C(3,2) ways=3Determine the values of a, b, and c for the quadratic equation 4x 2 – 8x = 3 answer choices a = 4, b = 8, c = 3 a = 4, b =8, c =3 a = 4, b = 8, c = 3 a = 4, b = 8, c = 3 s Question 2
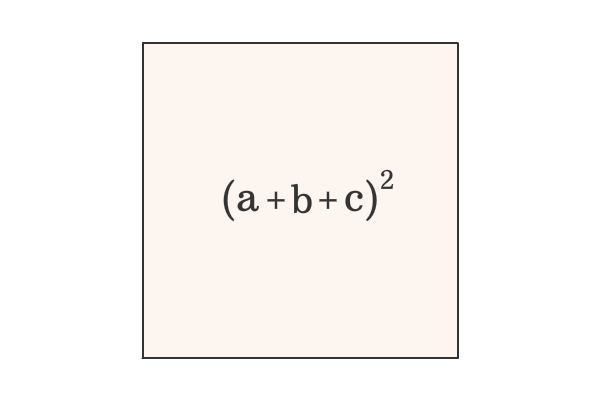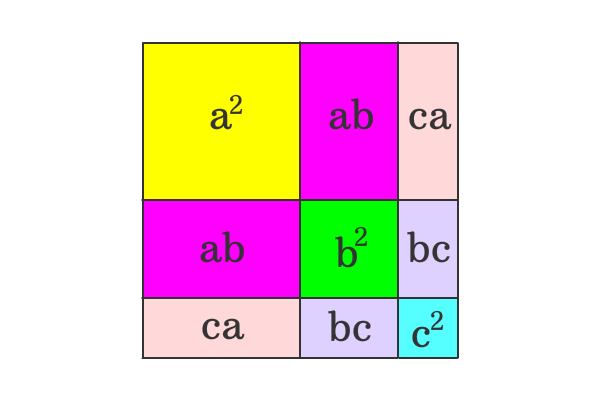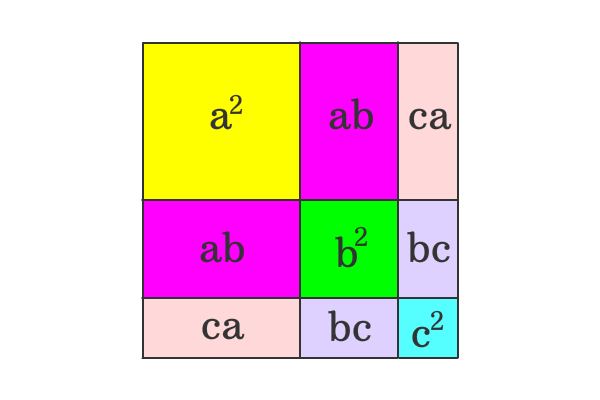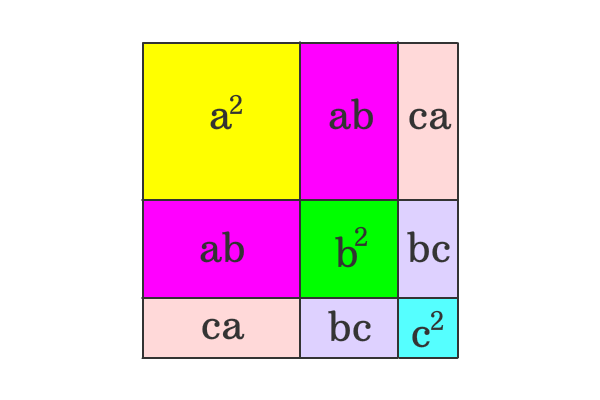


Proof Of A B C Formula In Geometric Method



Maths Formulas For Class 9 Important Class 9 Mathematics Formulas
A³ b³ = (a b)(a² – ab b²) you know that (a b)³ = a³ 3ab(a b) b³ then a³ b³ = (a b)³ – 3ab(a b) = (a b)(a b)² – 3ab = (a b)(a² 2ab b² – 3ab) = (a b)(a² – ab b² ) Please log inor registerto add a comment Related questionsAnd we must go thru the formulae sequentially a (BC)2 ≡ ()2(B5C2−)2 the charge on this species is 10 so this is not a contender b A3(BC4)2 ≡ ()3(B5C2− 4)2 the charge on this species is 0 so this is a contender${\left( {a b c} \right)^2} = {a^2} {b^2} {c^2} 2ab 2ac 2bc$ ${\left( {a b} \right)^3} = {a^3} 3{a^2}b 3a{b^2} {b^3};{\left( {a b} \right)^3} = {a^3} {b^3} 3ab\left( {a b} \right)$ ${\left( {a b} \right)^3} = {a^3} 3{a^2}b 3a{b^2} {b^3}$ ${a^3} {b^3} = \left( {a b} \right)\left( {{a^2} ab {b^2}} \right)$
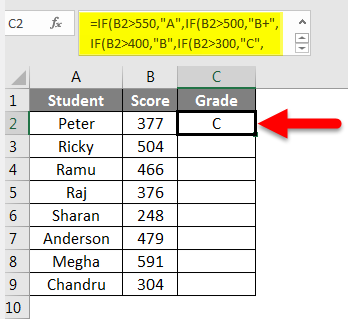


Formula For Grade In Excel How To Use Formula For Grade In Excel


2
4 years ago A B C 3 Formula Source (s) https//shrinkurlim/badse DanielM Lv 4 1 decade ago This is just multiplying out and bookkeeping It's a^3 b^3 c^3 plus 3 of each term having oneTriangle= \frac{1}{2}bh\ Where, b is the base of the triangle h is the height of the triangle If only 2 sides and an internal angle is given then the remaining sides and angles can be calculated using the below formula${\left( {a b c} \right)^2} = {a^2} {b^2} {c^2} 2ab 2ac 2bc$ ${\left( {a b} \right)^3} = {a^3} 3{a^2}b 3a{b^2} {b^3};{\left( {a b} \right)^3} = {a^3} {b^3} 3ab\left( {a b} \right)$ ${\left( {a b} \right)^3} = {a^3} 3{a^2}b 3a{b^2} {b^3}$ ${a^3} {b^3} = \left( {a b} \right)\left( {{a^2} ab {b^2}} \right)$



Multinomial Expansion


How To Subtract In Excel Cells Columns Percentages Dates And Times



Matrices Class 12 Formulas And Notes Vidyakul



A B C Whole Cube A Cube B Cube C Cube 3 A B B C C A Prove It Plzzzz I Need It Today Brainly In



Heron S Formula Wikipedia



Just Say Me Exact Formula Of A B C Whole Cube Brainly In


3
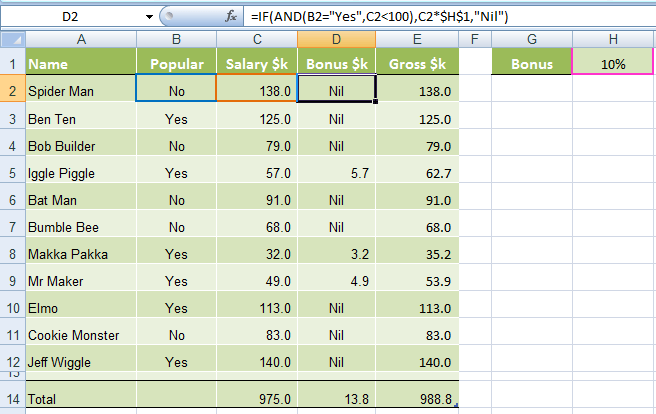


Excel If And Or Functions Explained My Online Training Hub



Using The Quadratic Formula Number Of Solutions Video Khan Academy
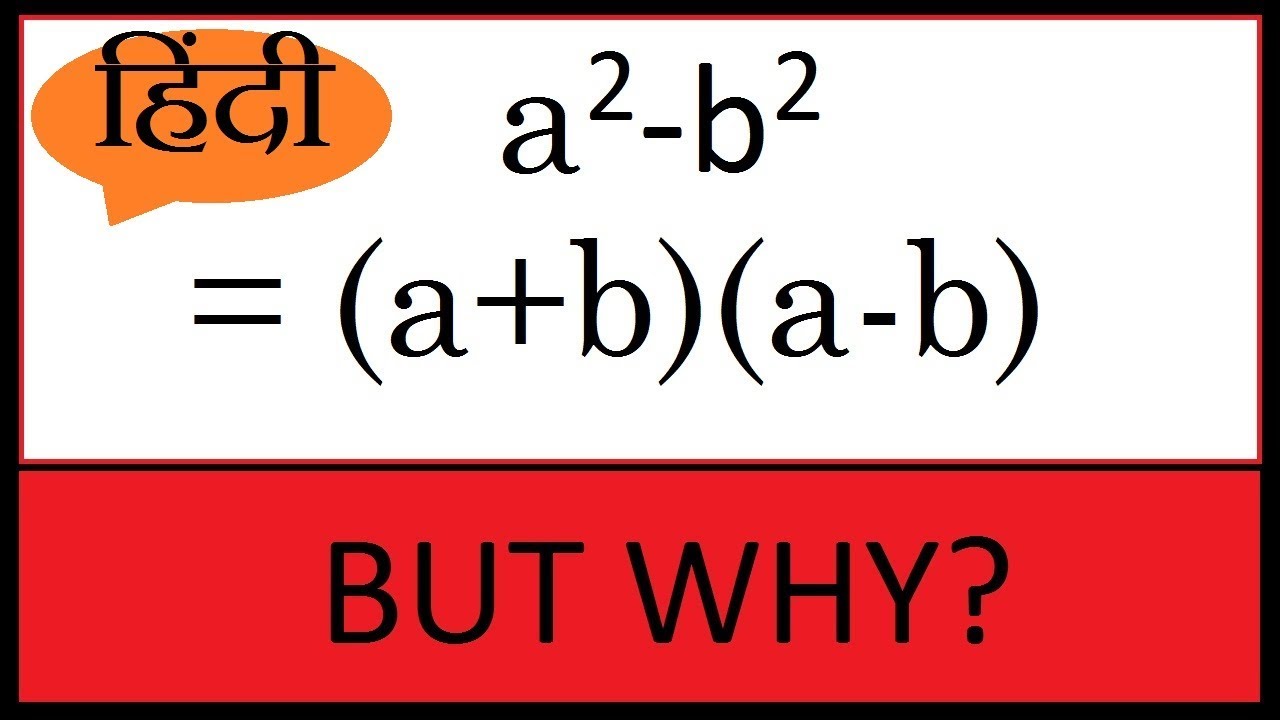


A Square Minus B Square Formula In Hindi Youtube
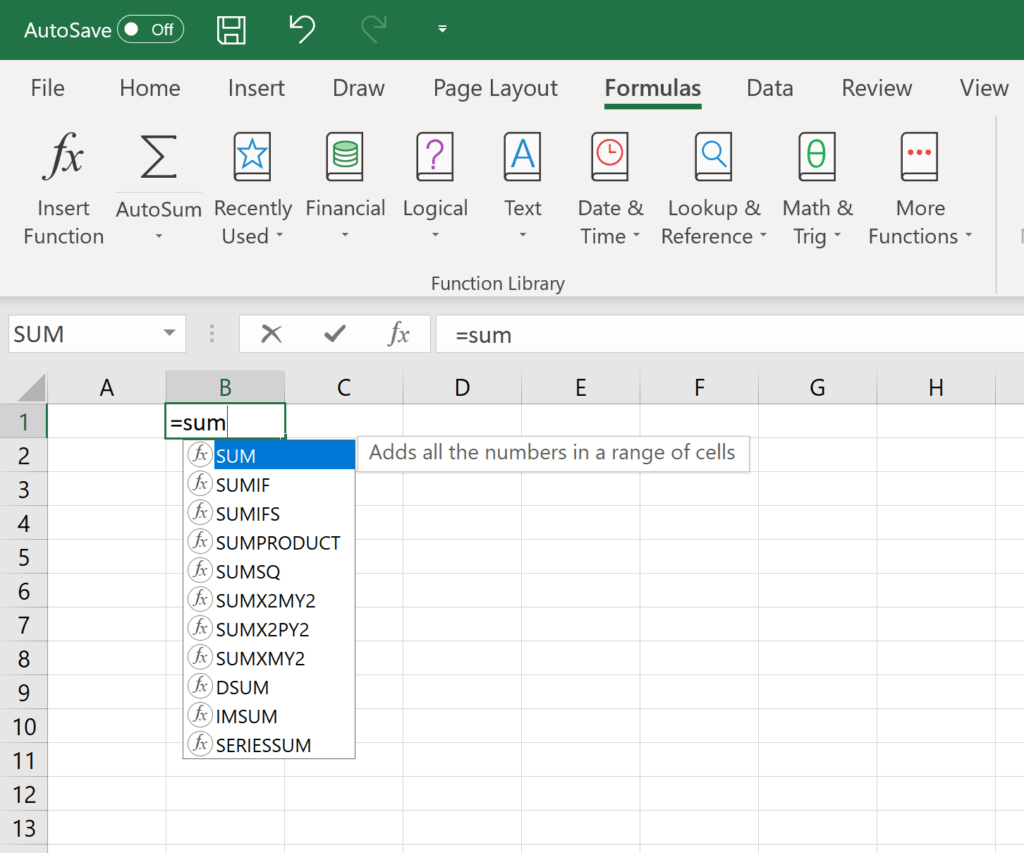


Basic Excel Formulas List Of Important Formulas For Beginners



What Are Various Forms To Write A B C A Whole Cube Quora



17 Math Ideas Math Math Formulas Studying Math



Ncert Class 9 Maths Lab Manual Verify The Algebraic Identity A B C A B C 2ab 2bc 2ca Cbse Tuts



Algebra Formulas A B 3 A B 2 A B C 3 A 3 B 3 Teachoo


What Is The Expansion Of A B C 3 Quora


Www Math Brown Edu Jhs Frintch1ch6 Pdf


What Is The Formula Of Math A 3 B 3 Math Quora
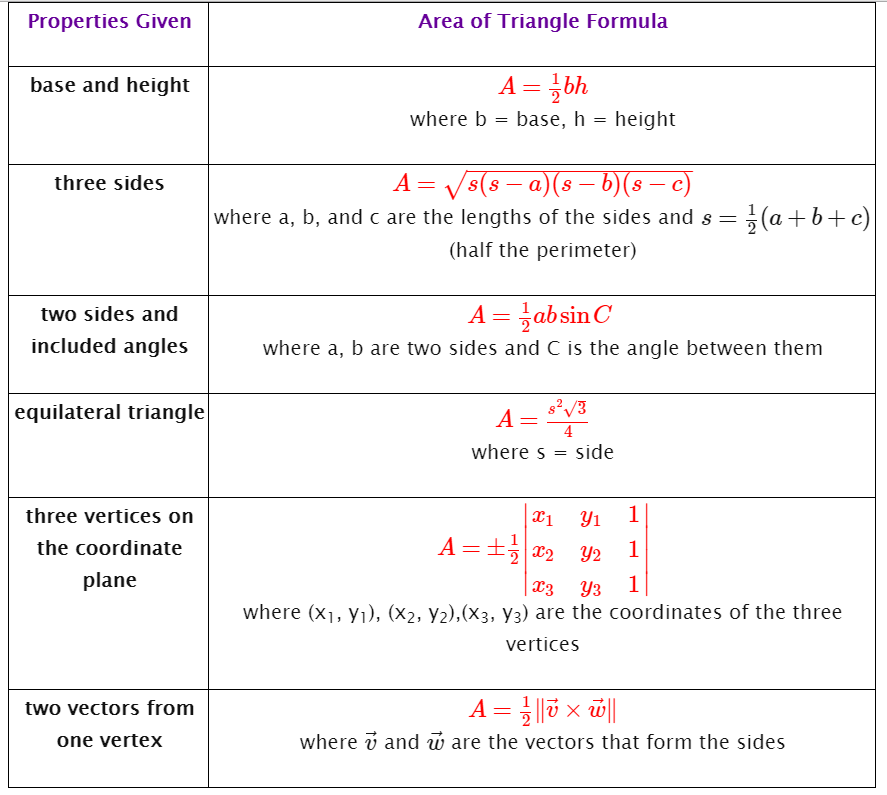


Area Of Triangles Formulas Video Lessons Examples Step By Step Solutions



Excel Formula For Grade How To Calculate Letter Grades In Excel
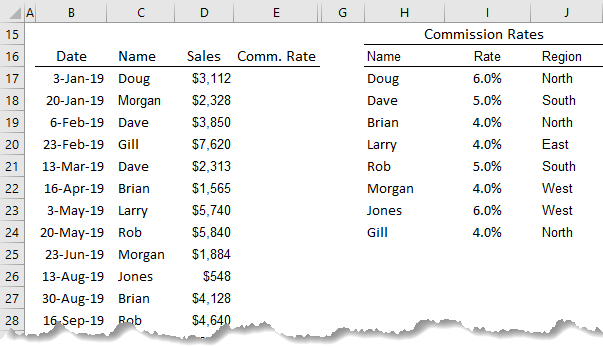


Excel Vlookup Formulas Explained My Online Training Hub


If B2 C2 Ab Ca 0 Prove That A B C Polynomials Maths Class 9


What Is The Formula For A 3 B 3 Quora



Algebra Formulas A B 3 A B 2 A B C 3 A 3 B 3 Teachoo



Pythagorean Triple Wikipedia


Cbse 10 Math Cbse Coordinate Geometry Ncert Solutions



Class 7 Maths Formulas Download All Math Formulas Cuemath



The Value Of A Cube Plus B Cube Plus C Cube Minus 3 Abc If A B C Is Equals To 15 And A B Ca Brainly In


Evaluate The Formula Vectors A X A X C A C B A B C If Sarthaks Econnect Largest Online Education Community



Algebra Formulas A B 3 A B 2 A B C 3 A 3 B 3 Teachoo



Suka Chemistry Acid And Base Calculations Formula


Q Tbn And9gcsn3hmt8qz Utmzoqeyjo2k4rnk95kuib8fxbhmd Uvs2llqap Usqp Cau


Math Scene Equations Iii Lesson 2 Quadratic Equations



The Binomial Theorem Binomial Expansions Using Pascal S Triangle Subsets



Example 5 Find Values Of A B C D 2a B A 2b Examples


What Is The Expansion Of A B C 3 Quora
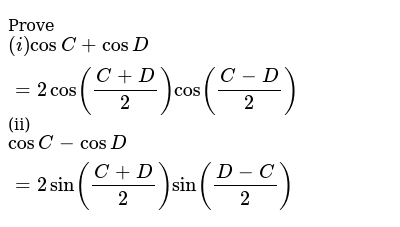


Prove I Cos C Cosd 2cos C D 2 Cos C D 2 Ii Cosc Cosd 2si



Cbse Board Exam 21 Check Class 10 Maths Important Formulas For Quick Revision


A B 3
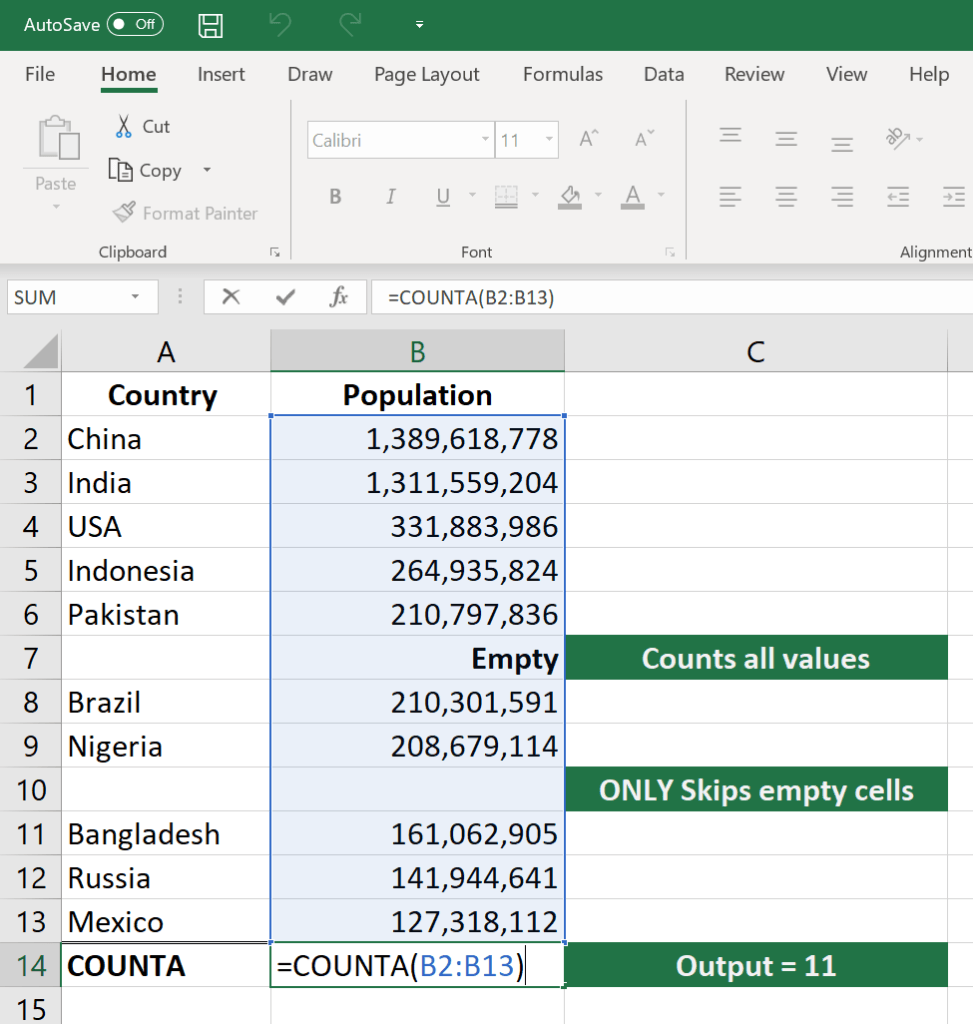


Basic Excel Formulas List Of Important Formulas For Beginners


What Is The Formula For Math A B C 3 Math Quora



3 Ways To Calculate The Circumference Of A Circle Wikihow



Cbse Class 11 Maths Chapter 3 Trigonometric Functions Formulas


What Is The Formula Of A B C A Whole Cube Quora



Handa Ka Funda Math Formulas 5 0



What Are Various Forms To Write A B C A Whole Cube Quora



Heron S Formula Wikipedia
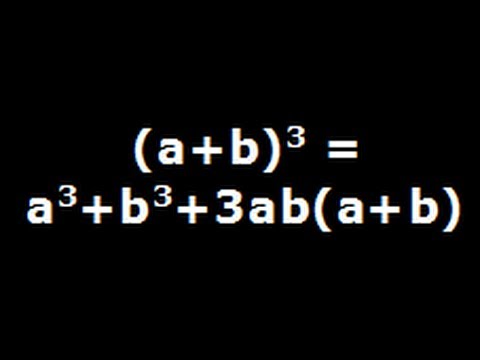


A Plus B Cube Algebra Identity Explained Step By Step Youtube



Formula Of A3 C3 Brainly In
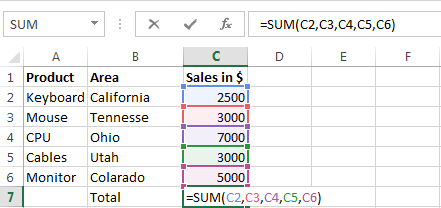


Top 10 Excel Formulas Asked In An Interview Answers



What Is The Expansion Of A B C 3 Quora
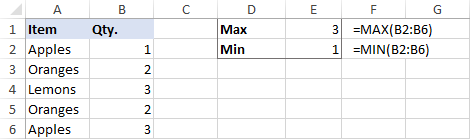


Basic Excel Formulas Functions With Examples


What Is The Formula Of Math A 3 B 3 Math Quora



Solved Given Ka H Minit And That Pka 3 75 C Chegg Com



Final Exam Exercises 1 The Element In Group 3a And Period 3 Is Ppt Download



What Are Various Forms To Write A B C A Whole Cube Quora


What Is The Formula For Math A B C 3 Math Quora



Solved Ekeess Bry Ec B U Ll The Conversion Of 2 Butyne Chegg Com



How To Use The Excel Sum Function Exceljet



Acids Exam Problems M C 260
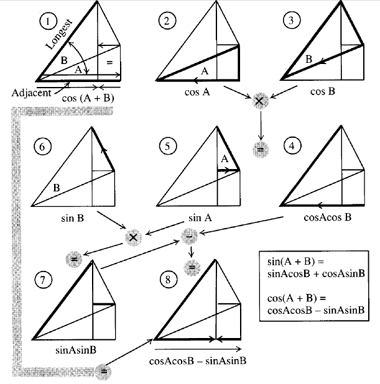


Trigonometric And Geometric Conversions Sin A B Sin A B Sin Ab



Proof Of Formula Of Whole Cube Of A B C A B C 3 Youtube
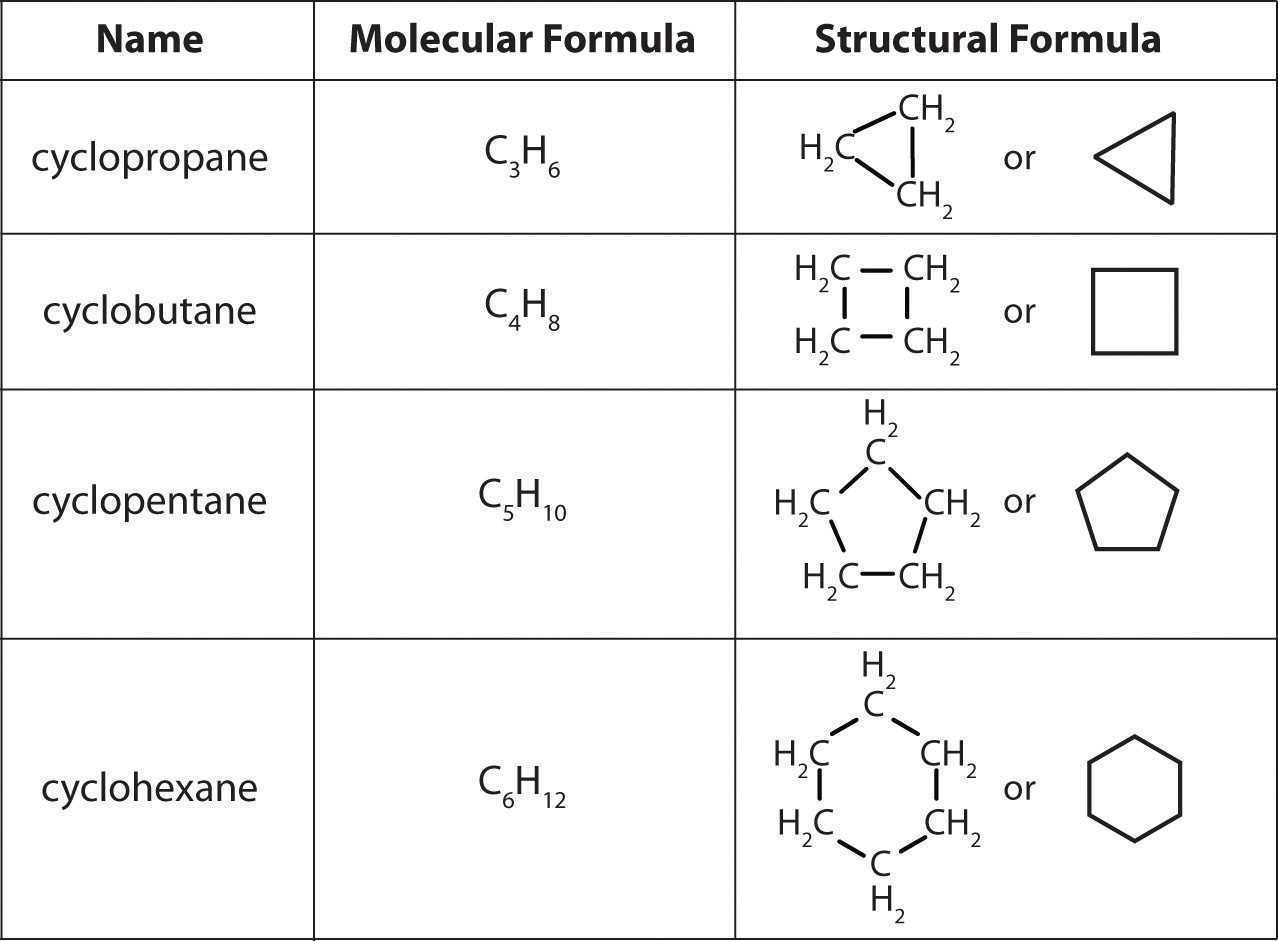


3 7 Names Of Formulas Of Organic Compounds Chemistry Libretexts


Q Tbn And9gcrwxskagpy6lndt5stu6oxp1 K0tw6brabfeaf Ncwojlvhrcb Usqp Cau
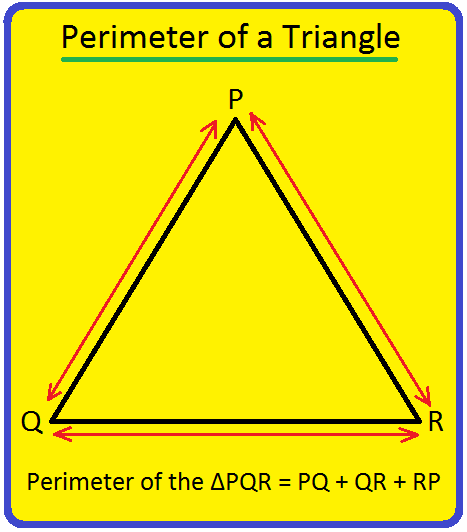


Perimeter Of A Triangle Perimeter Of A Triangle Formula Examples



Proof Of Formula Of Whole Cube Of A B C A B C 3 Youtube
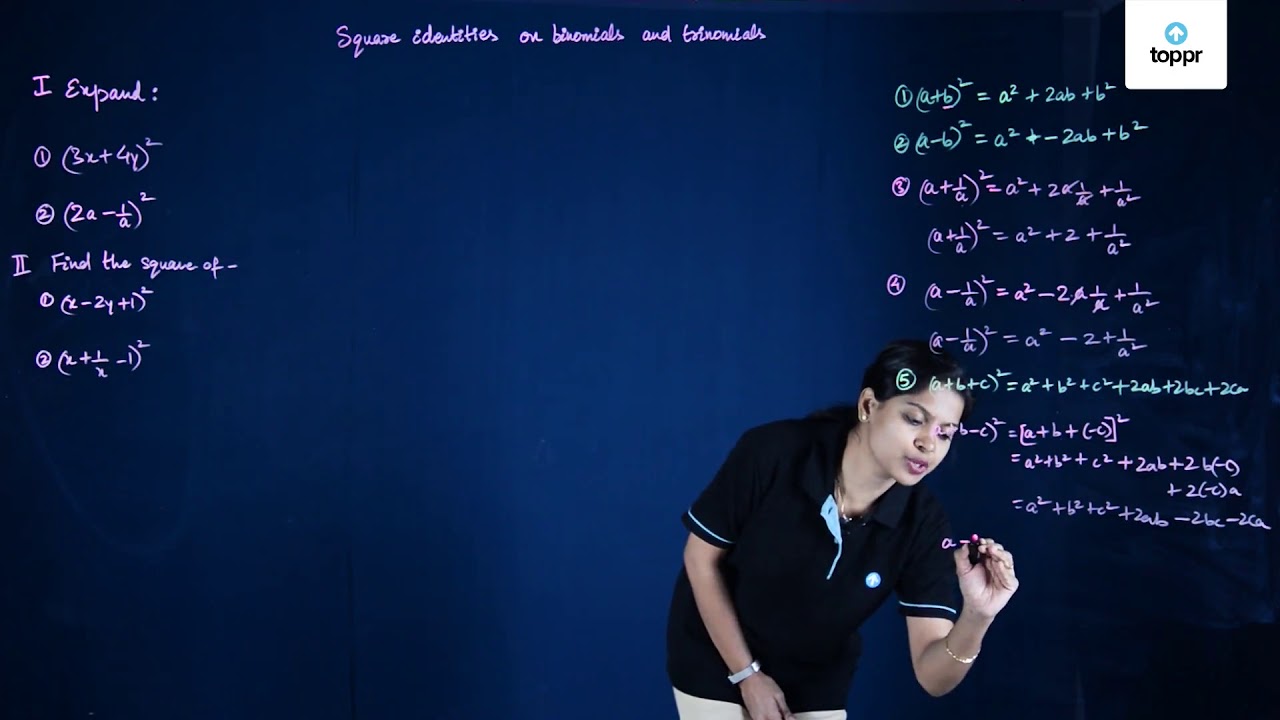


Standard Identities Of Binomials And Trinomials Equations Examples
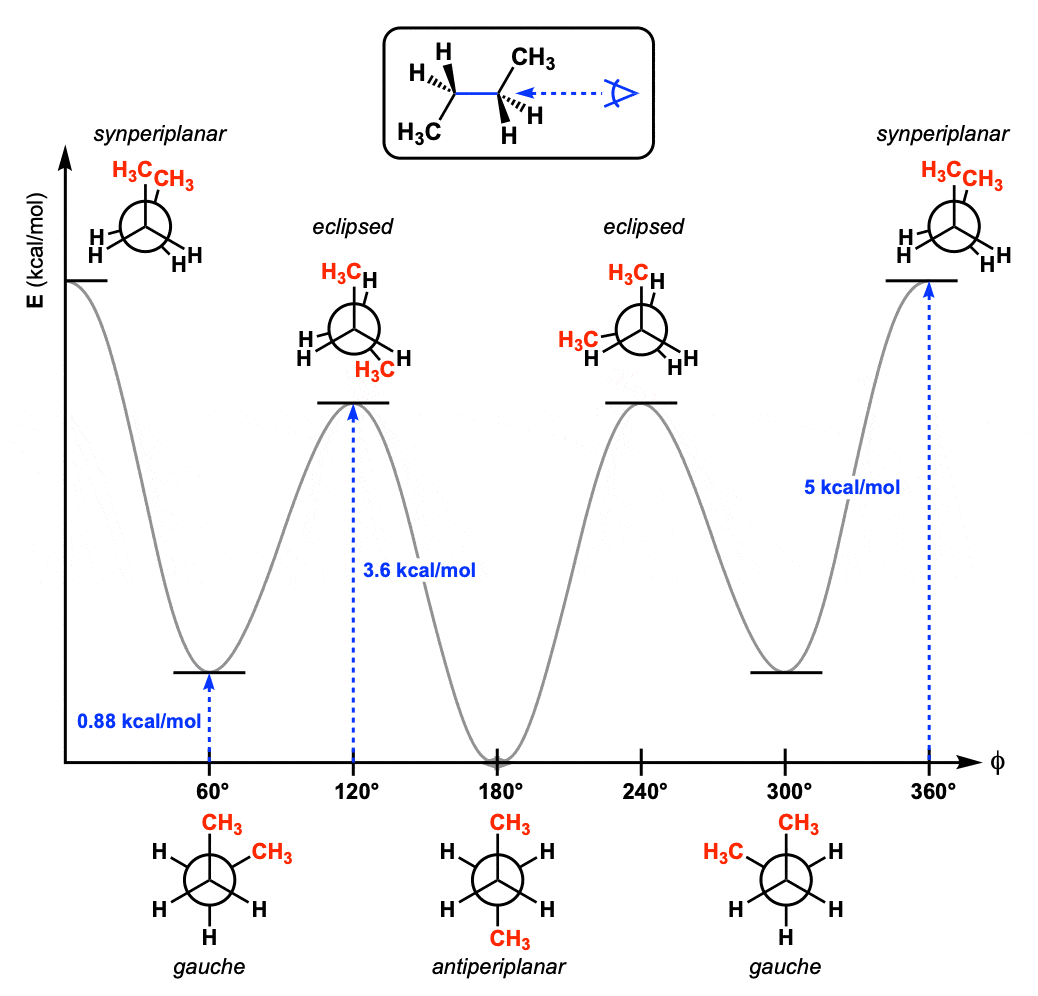


Newman Projection Of Butane And Gauche Conformation



Misc 13 Using Determinants 3 A B C Ab Ac
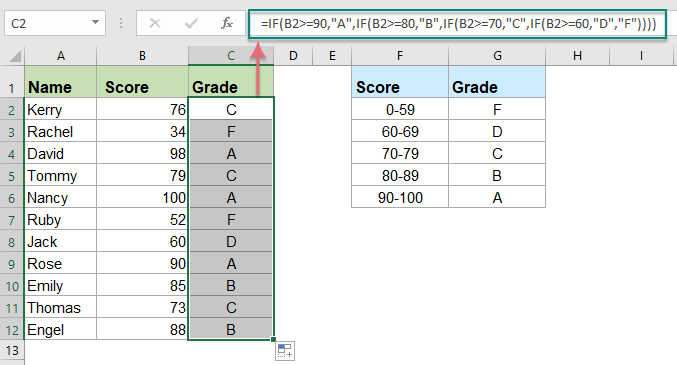


How To Calculate Or Assign Letter Grade In Excel


Www Madison Lake K12 Oh Us Userfiles 680 Classes Ied Review engineering formula sheet Pdf
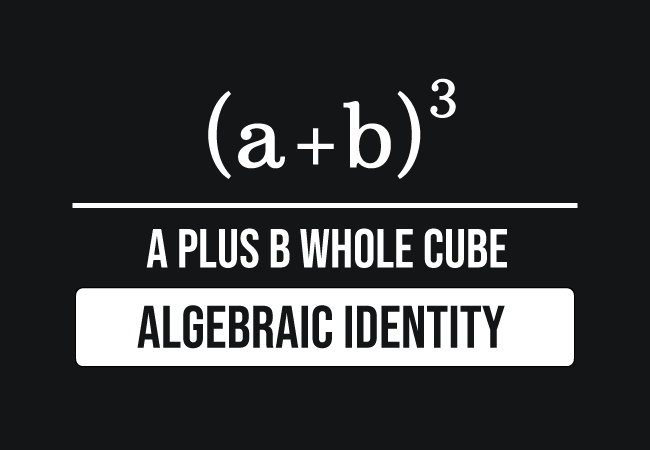


A B Formula Identity
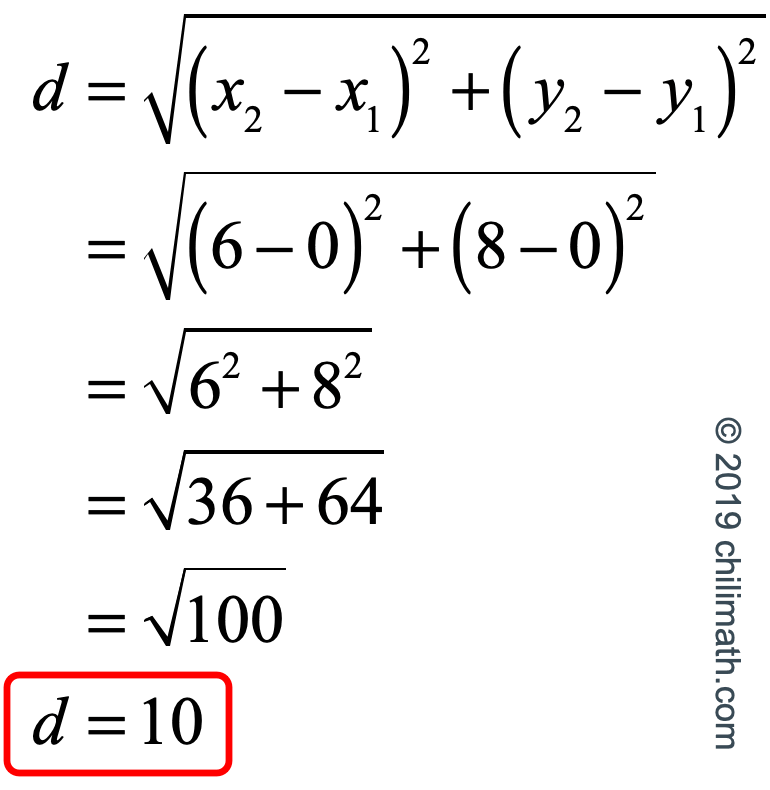


Distance Formula Chilimath


Illustrations Of Formulas
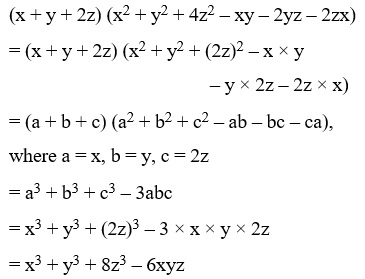


Algebraic Identities Of Polynomials A Plus Topper



Algebra Formula Definition Formulas And Examples



What Are Various Forms To Write A B C A Whole Cube Quora


Math Help Algebra Quick Algebra Formulae Technical Tutoring



What Are Various Forms To Write A B C A Whole Cube Quora



Prove A3 C3 3abc A B C B2 C2 Ab Ac Youtube
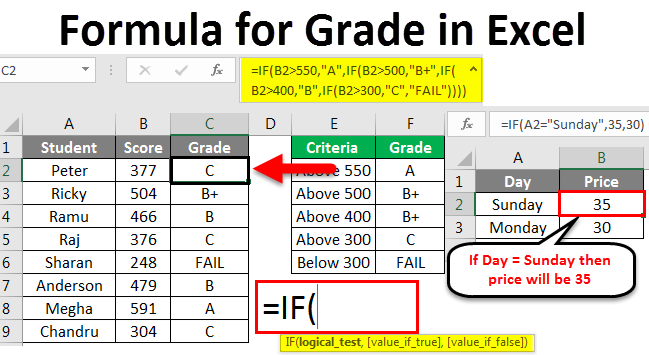


Formula For Grade In Excel How To Use Formula For Grade In Excel



Answers Key To Exam 3 Principles Of Chemistry I Chm 211 Docsity



Solved 32 What Are The Correct Chair Chair Present Many Chegg Com



A Plus B Ka Whole Cube Pdf Download Ssc Result
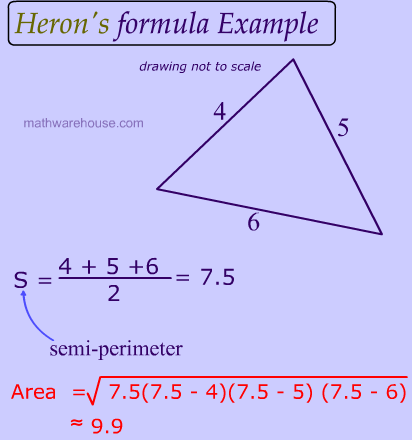


Herons Formula Explained With Pictures Examples And Practice Problems
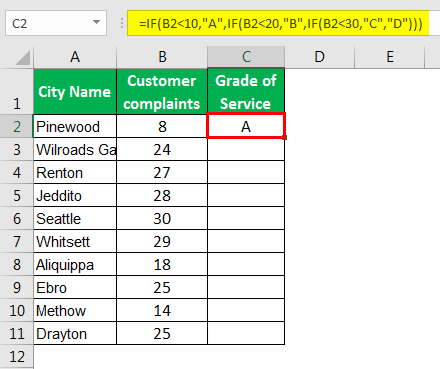


Excel Formula For Grade How To Calculate Letter Grades In Excel


コメント
コメントを投稿